We demonstrate a possibility of using fractal analysis methods for understanding nonlinear dynamical mechanisms of catastrophic events in economic systems and quantifying their global stability. Based on an analysis of floating currency exchange rates in more than 30 countries for a 10-year period, it is found that deviations of national monetary systems from optimally stable states correlate with deviations of the detrended fluctuation analysis (DFA) index of currency fluctuations from its normal value of 1.5 satisfying the efficient market hypothesis. The observed dependence is used for classifying long-term stability of national currencies as well as for revealing various forms of distortion of stable currency dynamics prior to large-scale crises. It is shown that monetary crashes are usually preceded by prolonged periods of abnormal (decreased or increased) DFA index values, with its after-crash value tending to 1.5, which is characteristic of stable exchange rate dynamics. The range of the DFA index consistent with crisis-free long-term exchange rate fluctuations is determined, and several typical scenarios of currency dynamics beyond this range are identified. Statistically significant relations (R=0.99, р<0.01) between the duration and the magnitude of currency crises considered as functions of the degree of distortion of stable fractal pattern of exchange rate dynamics are found and interpreted in terms of the self-organized criticality framework. The regression parameters of the obtained relations are shown to be nearly equal for both small-scale and large-scale crises indicating a possibility of a common instability mechanism of these events, and are used as a basis for forecasting of monetary crisis magnitude and duration over various time scales. For determination of the forecast accuracy and reliability, the statistics of ratios between predicted and measured values of both parameters has been investigated. The resulting average rations for in-sample forecasting of crisis magnitude are 101.8%7.7%, р<0.05 for increased DFA index and 100.8%2.5% for decreased DFA index. The duration forecasting has provided wider confidence intervals (102.9%15.3% and 103.9%8.8%, correspondingly), which can be related with interference of national governments during the post-crisis period. The developed technique can be used for real-time monitoring of dynamical stability of floating exchange rate systems and creating advanced early-warning-system models for currency crisis prevention.
O. Y. Uritskaya. Forecasting of Magnitude and Duration of Currency Crises Based on Analysis of Distortions of Fractal Scaling in Exchange Rate Fluctuations // Noise and Fluctuations in Econophysics and Finance. Eds. D.Abbott, J.-Ph.Bouchaud, X.Gabaix. – Proc. SPIE Vol.5848, 2005. – p. 17-26 (Third SPIE International Symposium on Fluctuations and Noise (Austin, USA, 2005)).
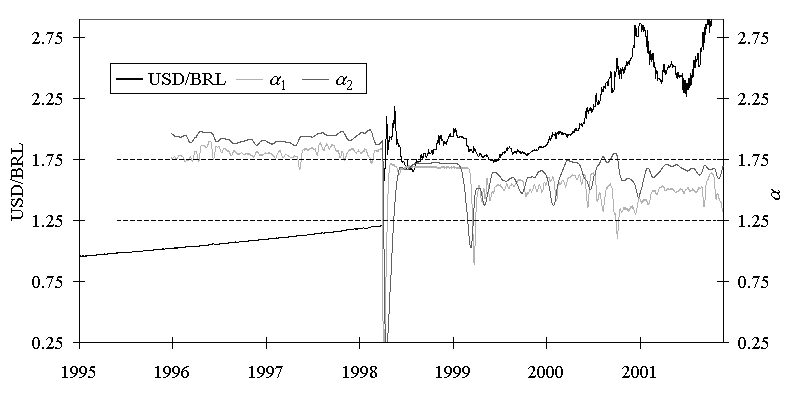
Fig. 1. Example of unstable currency dynamics (group Н, developing countries during periods preceding large-scale monetary crashes: Bulgaria, Brazil, India, Kazakhstan, Mexico, Russia, Rumania, Turkey, Ecuador) including a period of large-scale crisis. Before this event, DFA exponents had systematically increased values above the limit 1.75 of normal DFA exponent variations. After the crisis, both exponents returned to the interval [1.25, 1.75] signaling a normalization of dynamical stability of studied monetary system.
Fig. 2. Normalized crisis magnitude as a function of cumulative fractal indices characterizing the degree of fractal distortions in time series of exchange rate fluctuations with 2 < 1.25 (left) or 2 > 1.75 (right)
Fig. 3. Crisis duration (in days) as a function of the same parameters as in Fig. 2.